Factoring complex numbers is the process of breaking down a polynomial with real-valued coefficients into linear factors over the complex numbers. Every polynomial of degree n has n roots, counted according to their multiplicity.
This can be stated in root language as well. Complex numbers can be represented in the form z = u + v, where u and v are real numbers, the real and imaginary parts. By using complex numbers, quadratic polynomials can be factorized into two linear factors according to the fundamental theorem of algebra.
Factoring over the complex numbers is an important concept in algebra.
Introduction To Factoring Complex Numbers
Complex numbers can be factored into linear factors over the complex numbers, allowing for the decomposition of polynomials with real-valued coefficients. This concept is vital in understanding the roots and factors of complex polynomials.
What Are Complex Numbers?
Complex numbers are numbers that consist of a real part and an imaginary part. They can be represented in the form z = a + bi, where a is the real part and bi is the imaginary part. The imaginary unit i is defined as the square root of -1. Complex numbers are used in various branches of mathematics and physics to solve equations that involve both real numbers and imaginary numbers.
Understanding The Factor Theorem For Complex Numbers
The factor theorem for complex numbers states that every polynomial with real-valued coefficients can be factored into a product of linear factors over the complex numbers. In other words, if a polynomial has a complex root, then it can be factored using that root as a factor. This theorem is a powerful tool in solving polynomial equations with complex roots and simplifying complex expressions.
The Formula For Finding A Complex Number
The formula for finding a complex number in component form is z = u + vi, where u represents the real part and v represents the imaginary part. This formula helps in representing complex numbers as a combination of their real and imaginary components. The real part, u, is obtained by taking the real part of the given complex number, and the imaginary part, v, is obtained by taking the imaginary part. By using this formula, complex numbers can be easily manipulated and operated upon in various mathematical and engineering applications.

Credit: study.com
Methods Of Factoring Complex Numbers
Factoring complex numbers is a crucial step in solving equations involving complex numbers. It allows us to break down complex polynomials into simpler forms, making them easier to manipulate and analyze. There are several methods to factor complex numbers, each serving a unique purpose and solving specific types of equations. In this section, we will explore three common methods:
Factoring By Substitution
The method of factoring by substitution involves substituting a complex number with a different expression or variable that simplifies the polynomial. By carefully selecting a suitable substitution, we can break down complex polynomials into more manageable factors. This method is particularly useful when dealing with higher degree polynomials or complex equations. Let’s take a look at an example to understand this method better:
- Step 1: Identify a complex number within the polynomial that can be substituted.
- Step 2: Substitute the complex number with a simpler expression or variable.
- Step 3: Simplify the polynomial using the substitution and factor it further if possible.
- Step 4: Repeat the process until the polynomial is fully factored.
Factoring Out The Constant Terms
Factoring out the constant terms is a straightforward method that involves identifying and extracting the common constant factors from a polynomial. This method is useful when a polynomial contains terms with the same constants, allowing us to simplify the polynomial by extracting these common factors. Here’s an example demonstrating this method:
- Step 1: Identify the common constant factors present in the polynomial.
- Step 2: Divide each term of the polynomial by the common constant factor.
- Step 3: Factor out the common constant factor from the polynomial.
- Step 4: Simplify the polynomial further if possible.
Factoring The Polynomials
The method of factoring the polynomials focuses on breaking down complex polynomials into simpler factors using various techniques such as factoring by grouping, factoring by difference of squares, or factoring by sum of squares. This method allows us to express complex polynomials as a product of simpler polynomials, making them easier to manipulate and solve. Here’s an example outlining this method:
- Step 1: Identify any common factors within the polynomial, if present.
- Step 2: Use specific factoring techniques like factoring by grouping, difference of squares, or sum of squares to simplify the polynomial.
- Step 3: Continue factoring until the polynomial is fully simplified.
By utilizing these three methods of factoring complex numbers, we can efficiently solve complex equations and analyze polynomial expressions with ease. Each method offers a unique approach to tackle complex polynomials and plays a crucial role in solving equations involving complex numbers.
Factoring Complex Numbers Using Imaginary Unit
Complex numbers can be factored using the imaginary unit. This approach allows for the factorization of polynomials with complex roots, providing a comprehensive understanding of the polynomial equation. Explore various resources and calculators available to simplify the factoring process.
Introducing The Problem Of Factoring Sums Of Squares
Factoring complex numbers is a key concept in mathematics that allows us to break down polynomials into their simplest form. In this article, we will specifically explore the process of factoring sums of squares using the imaginary unit. By understanding this method, we can confidently solve complex numbers and further enhance our mathematical abilities.
Using The Imaginary Unit To Rewrite The Sum As A Difference
To factor sums of squares, we utilize the power of the imaginary unit, denoted as ‘i’. The imaginary unit is defined mathematically as the square root of -1. By substituting the imaginary unit for ‘i’ in our polynomial expression, we can transform the sum of squares into a difference. This crucial step lays the foundation for further factoring.
Factoring The Difference Of Squares
Once we have rewritten the sum of squares as a difference, we can proceed with factoring. The difference of squares is a special case that can be easily factored using a simple formula. By identifying the squares within our expression and applying the appropriate factoring method, we can simplify complex numbers into their prime factors.
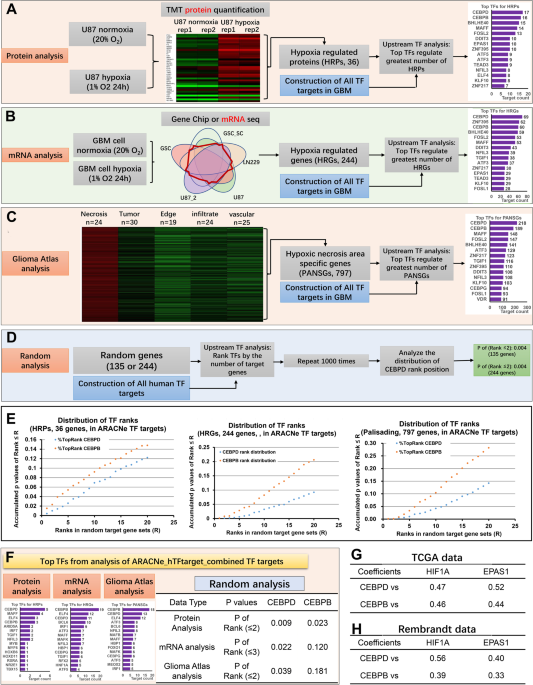
Credit: www.nature.com
Factoring Polynomials With Complex Roots
Complex Roots are an essential aspect of factoring polynomials. Every polynomial with real-valued coefficients can be factored into a product of linear factors over complex numbers. This method is widely used to solve equations and find the roots of polynomials.
Understanding Polynomials with Complex Roots In mathematics, polynomials with complex roots play a crucial role in various applications, especially in the field of algebra and calculus. A polynomial with complex roots can be factored into linear factors, providing valuable insights into the behavior and properties of the polynomial function. Applications of Factoring Polynomials with Complex Roots The process of factoring polynomials with complex roots finds extensive applications in engineering, physics, and signal processing. By factoring polynomials with complex roots, we can effectively analyze the behavior of systems described by polynomial functions and solve problems related to resonance, oscillations, and response to external stimuli. Examples of Factoring Polynomials with Complex Roots Example 1: Factoring the polynomial x^2 + 1 The given polynomial x^2 + 1 has complex roots ±i, where i represents the imaginary unit. By factoring this polynomial, we can express it as (x + i)(x – i), providing a clear representation of its complex roots. Example 2: Factoring the polynomial x^2 + 4x + 5 The quadratic polynomial x^2 + 4x + 5 does not have real roots, but it has complex roots -2 + i and -2 – i. Through factoring, the polynomial can be expressed as (x + 2 + i)(x + 2 – i), showcasing its complex roots. These examples demonstrate how factoring polynomials with complex roots facilitates a deeper understanding of their behavior and enables us to identify their complex roots efficiently. By delving into the understanding, applications, and examples of factoring polynomials with complex roots, we gain valuable insights into the intricate nature of polynomials and their roots, laying the foundation for advanced mathematical explorations.Practical Applications Of Factoring Complex Numbers
Complex numbers can be factored into a product of linear factors, and every polynomial of degree n with real-valued coefficients has n roots over the complex numbers. By utilizing complex numbers, you can efficiently factorize complex polynomials.
Solving Complex Equations
Complex number factorization allows for the efficient solving of complex equations by breaking down the equation into its linear factors. This method simplifies the complex equation solving process and aids in finding solutions quickly.Finding Complex Number Solutions To Quadratic Expressions
Factoring complex numbers helps in finding the complex number solutions to quadratic expressions. By breaking down the quadratic expressions into their linear factors, we can easily identify the complex number solutions, contributing to problem-solving efficiency.Real-world Examples Of Using Complex Number Factorization
Complex number factorization has real-world applications in various fields like electrical engineering, physics, and signal processing. In electrical engineering, it aids in analyzing alternating current circuits, while in physics, it is used in wave mechanics and quantum mechanics. Additionally, in signal processing, complex number factorization helps analyze and process various signals effectively. Complex number factorization plays a vital role in solving complex equations, finding solutions to quadratic expressions, and has practical applications in real-world scenarios. By simplifying the solving of complex equations and providing efficient methods for finding complex number solutions to quadratic expressions, it is an essential tool in various fields with real-world implications.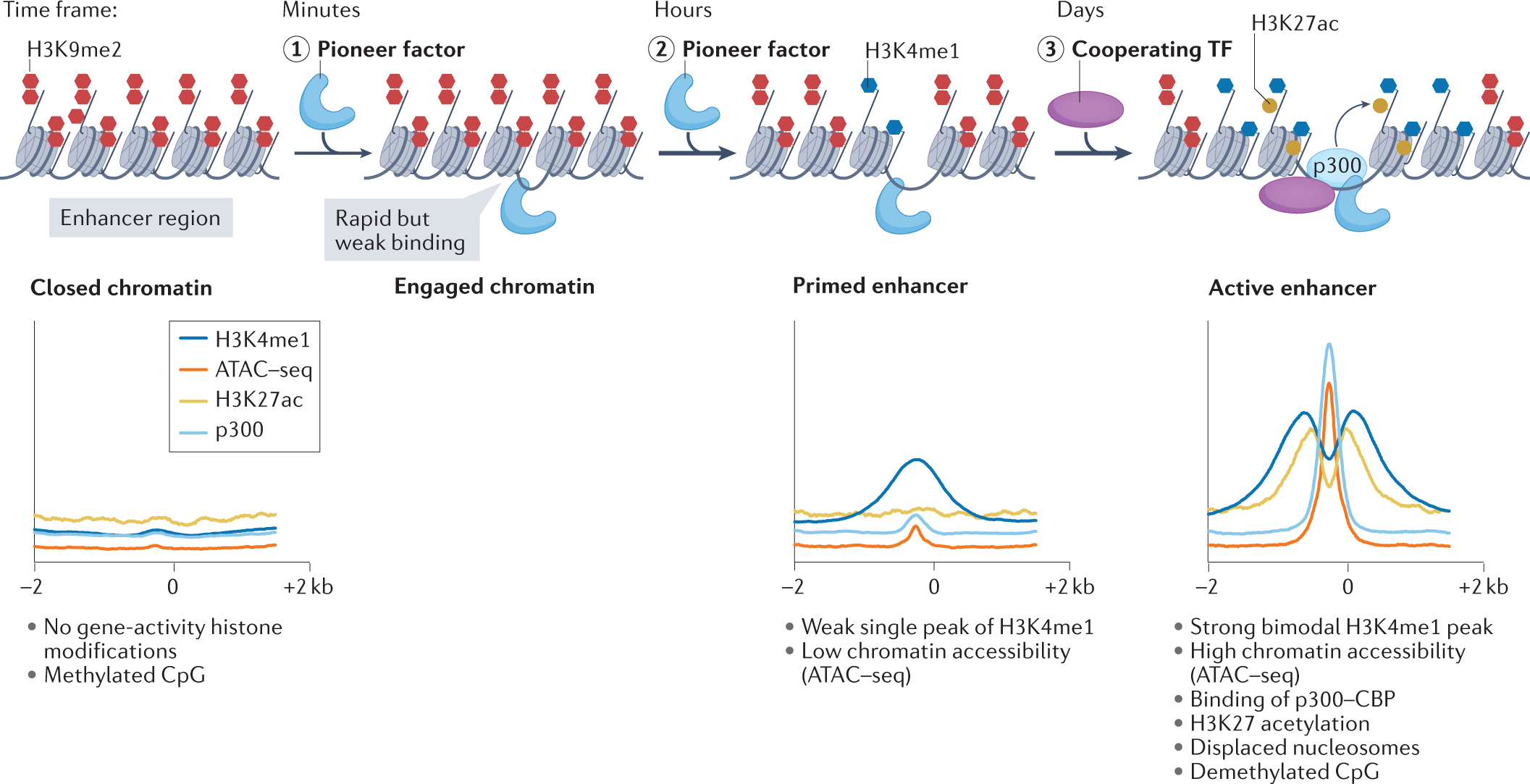
Credit: www.nature.com
Frequently Asked Questions For Factoring Complex Numbers
Can You Factor Complex Numbers?
Yes, over the complex numbers, every polynomial can be factored into a product of linear factors.
What Is The Factor Theorem For Complex Numbers?
The factor theorem for complex numbers states that every polynomial with real-valued coefficients can be factored into linear factors over complex numbers. This means that every polynomial of degree n has n roots in the complex number system.
How Do You Factor Complex Roots?
Complex roots can be factored by using the fundamental theorem of algebra, which states that every polynomial of degree n has n roots. This can be done by finding the factors of the polynomial, considering both the real and imaginary parts.
What Is The Formula For Finding A Complex Number?
To find a complex number, use the formula z = u + v, where u and v are real numbers representing the real and imaginary parts of the complex number. The formula u = Re@zD, v = Im@zD can also be used.
Complex numbers can be factored into a product of linear factors.
Conclusion
Factoring complex numbers plays a crucial role in mathematics. It allows us to break down polynomial equations into linear factors, providing valuable insights into their roots and multiplicities. By understanding the factor theorem for complex numbers, we can effectively factorize complex polynomials and solve equations.
This concept is essential in many fields, including algebra, geometry, trigonometry, and calculus. With the help of complex numbers, we can unravel the complexities of mathematical problems and broaden our understanding of the subject.